The FFT architecture includes a unique combination of block floating point (BFP) and floating point (FP) features that provide a much higher dynamic range than other other fixed-point FFT circuits with the same input word length. Typically, Centar’s circuits show ~6db/bit of dynamic range, where dynamic range is a measure of the difference between the smallest and largest detectable signals. For example, Fig. 1 below shows the outputs of two 256-point FFT circuits along with exact Matlab reference values. Both circuits receive the same16-bit “single tone,” real input block and produce 16-bit outputs plus an exponent. As can be see from Fig. 1, the Centar version provides ~96db of dynamic range between the two large coefficient outputs and other outputs, whereas the Altera version produces round-off noise that obscures the correct smaller outputs and therefore provides ~24db less dynamic range than its Centar equivalent.
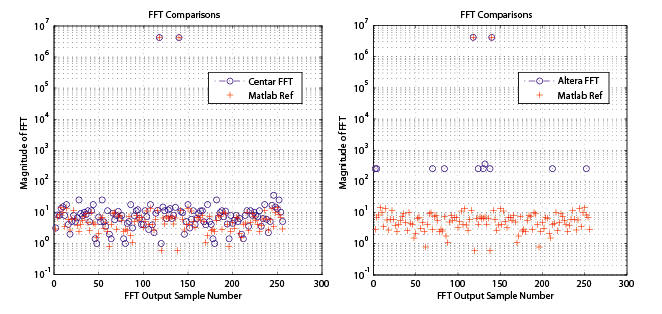
Fig. 1. Outputs of Centar (left) and Altera (right) 256-point fixed-size FFTs with 16-bit fixed-point
“single-tone,” real input data. Matlab computed reference output is also provided.
Most FFT circuits use fixed-point processing with either automatic scaling during the course of the computation or no scaling. In the former case dynamic range is sacrificed because scaling is not always necessary. In the latter case the word size can grow by as much as a factor of two, which increases usage of logic and memory resources, reduces the maximum clock rate and at the same time burdens all post-FFT processing with unnecessarily increased word lengths. A pure BFP is better because scaling is only performed when necessary, but requires more logic and memory resources than using fixed-point with automatic scaling and is limited in effectiveness due to the restriction of a single exponent per FFT block. Alternatively, our automatic FP/BFP approach provides typically 4 bits (~24db) of extra dynamic range compared to other BFP based schemes and even more compared to traditional fixed scaling per stage.
Because all the important processing occurs along horizontal PE rows, it is possible to add local circuitry to each so that during column DFT processing (Step 1 of the two step processing) all intermediate results are normalized to the same exponent using shifter circuitry in the multiplier PEs. Therefore, each of the each of the Nr rows of the N=Nr x Nc DFT matrix has its own BFP exponent. During the final row DFTs (Step 2) computation all results are computed using floating point without any further normalization, so that each output sample has its own exponent. For applications that require fixed-point inputs the output samples can be converted on-the-fly to pure BFP (single exponent for an entire FFT output data block.)
Fig.2. Illustration of multiple BFP regions in an array (b=4, N=1024, Nr=32, Nc=32).
As a of measure dynamic range capabilities, the DFT was computed using “single tone” input data (full range real sinusoids with random frequency and phase). This generates a complex conjugate output along with very small residual values (Fig. 1). The difference in magnitudes of the main output and residual values is a measure of the the circuit’s potential dynamic range. The dynamic range is computed here in two ways for better characterization of the circuit. The first measure of dynamic range (DR1) is the ratio of the power associated with the complex conjugate outputs and the power of the maximum noise value or
DR1 = 10 log10 (zs2 / max(z(n))2)
where zs is the complex conjugate output power and z(n) are the other N circuit and reference values. This measure is useful because it can distinguish large “spikes” in the N-2 roundoff noise values, which could obscure a similar size small “real” signal. Next DR2 measures the signal output with respect to the total roundoff noise. This is computed by summing the signal power of the single complex conjugate output and dividing by the sum of the roundoff noise output powers:
DR2 = 10 log10 (zs2 / ∑n (z(n)-zref(n))2)
where zref(n) are the “correct” reference FFT outputs. The results for DR1 and DR2 presented below in Table 1 are based on 16-bit fixed-point input data (16-bit output mantissa and 5-bit output exponents).
| Transform Size | DR1 | DR2 | ||||||
| mean | max | min | std dev | mean | max | min | std dev | |
| 128 | 103 | 117 | 94 | 2.76 | 97 | 112 | 94 | 3.09 |
| 256 | 105 | 111 | 95 | 2.32 | 97 | 130 | 92 | 2.64 |
| 512 | 104 | 141 | 95 | 4.73 | 97 | 102 | 90 | 2.51 |
| 1024 | 105 | 111 | 96 | 2.29 | 94 | 121 | 90 | 2.18 |
| 2048 | 105 | 118 | 98 | 2.36 | 95 | 111 | 89 | 1.81 |
Table 1. Dynamic range DR1 and DR2 comparisons for different FFT sizes with 16-bit input data. (Results obtained as averages over >1000 different random frequency and phase input data sets).
Generally the DR2 results show that the total round-off noise power is ~6db/bit below the maximum signal outputs and DR1 shows that the round-off noise “floor” is >100db down from maximum signal magnitude).


