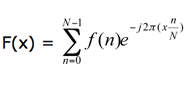CENTAR » Algorithm

Technology: Algorithm

To compute the discreet Fourier transform (DFT) the traditional “row/column” approach is used. This factorization assumes the transform size N can be written the product N =N₁*N₂ and requires computation of two sets of smaller DFTs, N₂ transforms of length N₁ (referred to as “column” transforms) and N₁ transforms of length N₂ (referred to as “row” transforms). The N₁xN₂ “DFT matrix” X contains input samples x_i that are arranged x₁,x₂,…,x_N2 on row 1, x_N2+₁,x_N₂₊₂,…,x_2*_N2, on row 2, etc. In between column and row transforms it is necessary to multiply each of the N points by the usual twiddle factor, W_N^i,k, i=0,1,..,N₁-1, k=0,1,..N₂-1. After the row transforms the DFT output Z resides in the matrix in column major order.

It remains to be shown how the N₂-point row and N₁-point column DFTs are computed. Centar’s approach is very different from the usual mapping of decimation-in-time and decimation-in-frequency “signal flow” graphs onto linear and parallel circuit structures. Rather a new matrix based algorithm is used to compute the DFT which naturally maps into a succession of radix-b matrix-matrix multiplications that can be done at high speed with minimal complexity using small, locally connected systolic arrays. This derivation starts with the definition of the DFT as

$Z(k)=\sum_{m=0}^{M-1}W_{M}^{mk}X(m)$

(1)

where M is the transform size (M=N₂ for the row DFTs and M=N₁ for the column DFTs), X(m) are the time domain input values, Z(k) are the frequency domain outputs and W_M=e^-j(2π/M). In matrix terms (1) can be represented as

$Z=CX$

(2)

where C is a coefficient matrix containing elements W_M^mk. If M can be factored as M=N₃*N₄, then using the reindexings m=m₁+N₃m₂ and k=k₁+N₃k₂ with m₁=0,1,…,N₃-1, k₁=0,1,…,N₃-1, m₂=0,1,…,N₄-1, k₂=0,1,…,N₄-1 , (1) becomes

$Z(k_{1}+N_{3}k_{2})=\sum_{m_{1}=0}^{N_{3}-1}(W_{N}^{m_{1}k^{_{1}}}\sum_{m_{2}=0}^{N_{4}-1}W_{N_{4}}^{m_{2}k_{1}}W_{N_{4}}^{m_{2}k_{2}N_{3}}X(m_{1}+N_{3}m_{2}))W_{N_{4}}^{m_{1}k_{2}}$

(3)

This expression can be considerably simplified by imposing the restriction that N₃/N₄ be an integer value so that (W_N4)^m2k2^N3=exp(-2πm₂k₂N₃/N₄)=1. For any particular value of m₁,k₁ the value of the inner parenthesis in (3), Y(k₁,m₁) can be evaluated from the dot product

$Y(k_{1},m_{1})=W_{N}^{m_{1}k_{1}}\left [ W_{N_{4}}^{0}\; W_{N_{4}}^{k_{1}}\; W_{N_{4}}^{k_{2}}\cdots \; W_{N_{4}}^{(N_{2}-1)k_{1}}\right ]\begin{bmatrix} X\left (m_{1} \right )\\ X\left (m_{1}+N_{3} \right )\\ X\left (m_{1}+2N_{3} \right )\\ ...\\ X\left (m_{1}+\left ( N_{2}-1_{}\right )N_{3} \right ) \end{bmatrix}$

so that (3) becomes

$Z(k_{1}+N_{3}k_{2})=\sum_{m_{1}=0}^{N_{3}-1}Y(k_{1},m_{1})W_{N_{4}}^{m_{1}k_{2}}$

(4)

All the (N₃)² dot product values Y(k₁,m₁) can be collected in the N₃xN₃ matrix Y_b by performing the matrix multiplication

$Y_{b}=W_{M}\cdot C_{M1}X_{b}$

(5)

where W_M is an N₃xN₃ matrix with elements W_M[k₁,m₁]=W_M^m1k1, C_M1 is an N₃xN₄ coefficient matrix with elements C_M1[k₁,m₂]=W_M^m2k1 , X_b is an N₄xN₃ matrix with elements X_b[m₂,m₁]=X(m₁+N₃m₂), Y_b is a N₃xN₃ matrix with elements Y_b[k₁,m₁]=Y(k₁,m₁) and “•” means element-by-element multiply.

In a similar way for a particular k₁,k₂ the corresponding Z(k₁,N₃k₂) can be calculated from the dot product

$\small Z(k_{1}+N_{3}k_{2})=\left [ W_{N_{4}}^{0}\; W_{N_{4}}^{k_{2}}\; W_{N_{4}}^{2k_{2}}\cdots \; W_{N_{4}}^{(N_{3}-1)k_{2}}\right ]\begin{bmatrix} Y\left (k_{1},0 \right )\\ Y\left (k_{1},1 \right )\\ Y\left (k_{1},2 \right )\\ ...\\ Y\left (k_{1},\left ( N_{3}-1_{}\right ) \right ) \end{bmatrix}$

(6)

and by collecting the dot products as before, a matrix expression for calculating Z is obtained as

$Y_{b}=W_{M}\cdot C_{M1}X_{b};\; \; Z_{b}=C_{M2}Y_{b}^{t}$

(7)

where C_M2 is an N₄xN₃ coefficient matrix with elements C_M2[k₂,m₁]=W_M^m1k2 , and Z_b is an N₄xN₃ matrix containing the transform outputs Z_b[k₂,k₁]=Z(k₁+k₂N₃).

The character of (7) is determined largely by the value of N₄ or the “base” b (b=N₄) because this sets the reachable values of M and the structure of the coefficient matrices C_M1 and C_M2. In (7) C_M1 and C_M2 contain M/b² sub-matrices C_B=[c₁|c₂|...|c_b] with the form C_M1=[C_B^t|C_B^t|...|C_B^t] ^t and C_M2=[C_B|C_B|...|C_B] due to the periodicity of b or W_N4. Also, values of M are constrained to be integer multiples of b², since it was assumed in (3) that N₃/N₄ is an integer. Although the choice of b is application dependent, for power-of-two designs only “base-4” (b=4) designs are chosen because this choice provides good architectures that are arithmetically efficient. This selection results in

$c_{1}=\begin{bmatrix} 1\\ 1\\ 1\\ 1 \end{bmatrix}, c_{2}=\begin{bmatrix} 1\\ -j\\ -1\\ j \end{bmatrix},c_{3}=\begin{bmatrix} 1\\ -1\\ 1\\ -1 \end{bmatrix},c_{4}=\begin{bmatrix} 1\\ j\\ -1\\ -j \end{bmatrix},$

and

$C_{B}=\begin{bmatrix} 1 & 1& 1& 1\\ 1& -j& -1& j\\ 1 & -1& 1& -1\\ 1 & j& -1& -j \end{bmatrix}$

(8)

where C_B in (8) is the coefficient matrix for a 4-point DFT and also describes a radix-4 decimation in time butterfly. Therefore in (7) Y_b can be seen as resulting from a series of 4-point transforms of a bit-reversed input X followed by a twiddle multiplication and Z_b is obtained from summations of the results of 4-point transforms of (Y_b)^t.