The architecture of Centar’s FFT circuits for which the transform size is not a power-of-two (N≠2ⁿ) is based on a new matrix equation form of the discreet Fourier transform (DFT) which is derived using decimation in time and frequency.  For a transform length M, this form is

Y=W_b•C_M1 X

Z = C_M2 Y^t 

where W_b is an M/b x M/b  twiddle matrix, C_M1 is an M/b x b coefficient matrix, X is a b x M/b input matrix, C_M2 is a b x M/b coefficient matrix, Z is a b x M/b output matrix containing the transform outputs,  and “ •” means element-by-element multiply.  Typically b must be larger than the largest prime factor in the FFT factorization.  The matrices C_M1,C_M2 above contain one or more arrays of radix-b butterfly matrices C_B, e.g., C_M2=[C_B|C_B|...] and C_M2=[C^t_B|C^t_B|...]^t.

Functionally, the implementation of this matrix form can be mapped to a simple systolic (pipelined) structure containing two arrays for the matrix-matrix products (C_M1X and C_M2Y^t ) and a linear array of multipliers in between to do the element-by-element multiplies as shown in Fig. 1(a) and (b).  Here, C_M1 and Z are stored internally (in RAMs) and X and C_M2 flow into the array in pipelined fashion from the boundaries.  The length of the array is M/b, so it scales with transform size in the north-south direction in the figure.  Each small box in Fig. 1 is a processing element (PE) and contains a complex adder and multiplier, a couple of registers, a small memory and communicates locally with its neighbor.

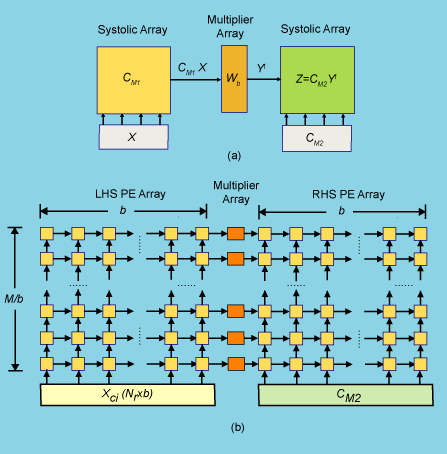
Fig.1 (a) Functional operation of architecture used to compute the DFT of M-points and (b) circuit implementation consisting of left hand side (LHS) and right hand side (RHS) arrays of elemental PEs, where each PE is symbolically contained within one of the yellow or red boxes.

The DFT transform is computed using the array in Fig. 1 to perform the well-known row/column factorization, N= N_r N_c , where N is the desired transform length and N_c and N_r are the number of columns/rows.  This approach requires calculation of two sets of DFTs, N_c  transforms of length N_r (referred to as “column” transforms) and N_r  transforms of length N_c  (referred to as “row” transforms).  In between column and row transforms it is necessary to multiply each of the N points by a corresponding twiddle factor,(W_N)^nk , n=0,1,..,N_c-1,  k=0,1,..N_r-1.  (Without the twiddle multiplication a 2‑D DFT is performed.)  The column and row DFTs are performed sequentially using the same hardware array with M=N_r for the column DFTs and M=N_c for the row DFTs.  For example to compute a DFT with 324 points, N=N_r N_c=36×9.  So here column DFTs would be done using the equation above with M=36 and b=6 followed by row DFTs with M=9 and b=3.  Note that an architecture as in Fig. 1 with b=6 can do both the row and column DFTs, but the row DFTs would use a smaller 3×3 subset of the b=6 array.  Therefore the advantage of working with an PE array that uses a larger value of b is that transforms with factors less than b can be done by using just a subset of the larger bxb element arrays, i.e, with an array structure using b=6, any transform of the form N=2ⁿ3^m4^p5^q6^r, where n,m,p,q and r are integers, is possible.

Finally, it is often advantageous to compute small DFTs with a mixed-radix.   For example Fig. 2 below shows an example of a case when the input data X corresponds to a sequence of 15-point DFTs, each represented by a 3×5

Fig.2 Data flow of architecture (b=6) used to compute DFTs of M=15 points (3×5). White boxes represent unused PEs.

 matrix.  In this case the processing is identical to the nominal case except that only the part of the PE arrays with “yellow” PEs are used.